
The square function is used by clicking on the "x^2" button or type "^2". The sign key (negative key) is used by clicking on the "(-)" button. The division (divide function) is used by clicking on the "/" button or using the keyboard "/" key. The multiplication (times function) is used by clicking on the "x" button or using the keyboard "*" key. The subtraction (minus function) is used by clicking on the "-" button or using the keyboard. The addition (sum function) is used by clicking on the "+" button or using the keyboard. Some of these features include: Unit Converter, Constants Library, Equation solver, Polynomial Solver, Base Conversion, and Decimal to Fraction Conversion. The pallet provides a display area for special features. The calculator is divided into two sections the scientific calculator interface on the left and the calculator pallet on the right.

Values in the stack can also be "popped" down into the input field of the calculator by clicking on the down arrows to the left of the line in the stack. The stack displays only 4 items at once, but one can scroll up and down the stack by clicking on the up and down arrow above the stack. The stack is a feature of the calculator that provides a way to view a history of results. The user is given the option to use either input method and both are equally valid however, there are some trigonometric function (as noted below) that are limited to computer keyboard entry only since there is a limited amount of space available for graphical button placements. The online calculator supports data entry through either a graphical button or through the use of traditional computer keyboard keys.

Expressions that contain parenthesis, such as "(1+2)*3", are evaluated by noting the precedence order and entering the form as "1 2 + 3 *". For example, to evaluate the expression "1 + 2" in RPN, the user is required to enter "1 2 +" and the expression is evaluated immediately after the operator. RPN Mode RPN, which stands for Reverse Polish notation, is a stack-based notation where operators are designed to follow their operands. Expressions entered in algebraic input mode are done in a manner that closely resembles the natural form of the expression and the order of the operations is determined by operator precedence and parenthesis. The calculator mode is set by clicking on the "ALG/RPN" symbol in the status bar or by changing the mode inside the menu dialog box.Īlgebraic input mode is commonly referred to as "infix notation" and is widely used by most handheld calculators. The online calculator operates in either algebraic input (default mode) or RPN input.
#Scientific unit conversion free#
eCalc is offered as both a free online calculator and as a downloadable calculator.

Inverse Cotangent Online Hyperbolic Trigonometric FunctionsĬoordinate System Decimal To Fraction Complex Numbers Online Unit Converter Constants Library Online Solver Base ConverterĮCalc is a free and easy to use scientific calculator that supports many advanced features including unit conversion, equation solving, and even complex-number math.
#Scientific unit conversion mac osx#
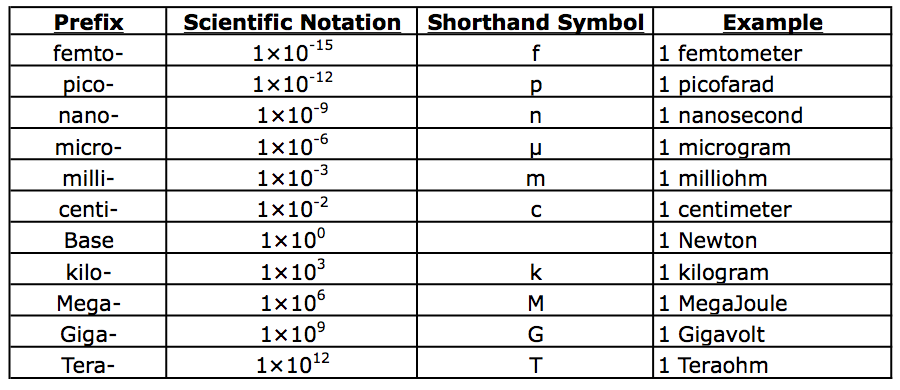
If you got at least half of those, you are doing a great job! With a bit more practice and you will be converting SI units with ease.Windows Version Mac OSX Version View More Downloads Using these two pieces of information, we can set up a dimensional analysis conversion.ĩ55\text Kilogram refers to 10 3 grams, while megagram refers to 10 6 grams. We will need two pieces of information from the table above. Let’s try converting 955 kilograms to megagrams. Here is an example of a one-step conversion between the SI system prefixes. Of course, you can always refer back to the tables above. Memorizing the different prefixes and their meanings makes it a lot easier to do these conversions, so try to memorize as many as you can. Interested in an Albert school license? Converting SI UnitsĬonverting between the different SI system prefixes is an essential science skill that requires practice. For example, speed can be measured in meters per second, or in kilometers per nanosecond. The different base units can also be combined to form what are called derived units. Instead, you would use kilometers or even megameters. For example, you wouldn’t measure the distance from LA to New York in meters, the base unit. These base SI units can be combined with any of the prefixes to create units that are most appropriate for what is being measured. These reference tables show the different bases and prefixes used to designate metric units with the SI system.


 0 kommentar(er)
0 kommentar(er)
